Project Euler https://projecteuler.net/ 有志による和訳Wiki http://odz.sakura.ne.jp/projecteuler/ をGitBookに写しているだけです。

ライセンス

CC BY-NC-SA 4.0です。

2020-7-29 GitBookからOpenSource活動として承認されました！

2020-7-16 和訳Wikiが消失していたことから、webarchiveからサルベージする事業を始めました。

https://project-euler-ja.gitbook.io/project-euler-ja/で公開しています。

メモ

• digit と number の訳し分けが出来ていないところがある。

• パンデジタル、などの用語の説明をまとめて書くとよいかも。

• 締めの言葉を統一したい。

• オリジナルへのリンクを忘れた。

• 何らかの問題が残っているページのタイトルには(*)が付けてある。

コントリビュート

PR welcome :)

• GitBook v2 の使い方についてはGitBook の公式ドキュメントを参照

• インラインの数式は $$...$$ というように囲む必要があるので注意

• VSCODE などのエディタ内で GitBook の数式をプレビューしたい場合は Markdown Preview Enhanced がオススメ。settings.json に以下の内容を追記すると良い感じに表示されます。

  "markdown-preview-enhanced.mathInlineDelimiters": [
    [
      "$$",
      "$$"
    ]
  ],
  "markdown-preview-enhanced.mathBlockDelimiters": [
    [
      "$$\n",
      "$$"
    ]
  ],

Project Eulerとは何ですか？

Project Eulerとは挑戦しがいのある数学/コンピュータプログラミングの問題集で、単なる数学的洞察だけではこれを解くことはできません。数学の知識があれば簡潔かつ効率的に問題を解くことができますが、多くの場合はコンピュータとプログラムの技能が必要です。

Project Eulerを開始し、また継続している動機は、未知の分野を探索し、愉快で楽しいコンテキストから新しい概念を学ぼうという探究心のためのプラットホームを提供することです。

これらの問題は誰を対象としていますか？

普通のカリキュラムでは飽きたらない学生、数学の専門家ではないが物事を数学的に扱うことに興味のある社会人、そして問題解決や数学の研鑽を積みたい専門家を想定しています。

誰でも問題を解くことができますか？

問題の難易度はさまざまです。多くの問題では帰納的連鎖学習(inductive chain learning)が期待されます。帰納的連鎖学習とは、一つの問題を解くことによって、新しいアイデアに触れることができ、それによって以前は解きようのなかった問題に着手することができるようになるということです。なので、やる気のある参加者ならば, ゆっくりではあるが着実に一問一問解いていくことができます。

次はどうしたら？

あなたの進行状況を記録するため、アカウントを設定しCookieを有効にする必要があります。すでにアカウントを持っていればを、でなければをお願いします。全て無料です！

どんな問題に挑戦するのか、登録する前にを見てみるのも良いでしょう。

フィボナッチ数列の項は前の2つの項の和である。最初の2項を1, 2とすれば、最初の10項は以下の通りである。

$1, 2, 3, 5, 8, 13, 21, 34, 55, 89, \dots$

数列の項の値が400万以下の、偶数値の項の総和を求めよ。

左右どちらから読んでも同じ値になる数を回文数という。2桁の数の積で表される回文数のうち最大のものは 9009 = 91 × 99 である。

では、3桁の数の積で表される回文数の最大値を求めよ。

13195の素因数は5, 7, 13, 29である。

600851475143 の素因数のうち最大のものを求めよ。

最初の10個の自然数について、その二乗の和は

$1^2 + 2^2 + \dots + 10^2 = 385$

最初の10個の自然数について、その和の二乗は

$(1 + 2 + \dots + 10)^2 = 3025$

これらの数の差は $3025 - 385 = 2640$ となる。

同様にして、最初の100個の自然数について二乗の和と和の二乗の差を求めよ。

2520 は 1 から 10 の数字の全ての整数で割り切れる数であり、そのような数の中では最小の値である。

では、1 から 20 までの整数全てで割り切れる数の中で最小の正の数はいくらになるか。

10以下の素数の和は $2 + 3 + 5 + 7 = 17$ である。

200万以下の全ての素数の和を求めよ。

ピタゴラス数（ピタゴラスの定理を満たす自然数）とは、 $a < b < c$ で以下の式を満たす数の組である。

$a^2 + b^2 = c^2$

例えば $3^2 + 4^2 = 9 + 16 = 25 = 5^2$ である。

$a + b + c = 1000$ となるピタゴラスの三つ組が一つだけ存在する。 これらの積 $abc$ を答えよ。

次の1000桁の数字のうち、隣接する4つの数字の総乗の中で最大となる値は$9 \times 9 \times 8 \times 9 = 5832$である。

73167176531330624919225119674426574742355349194934
96983520312774506326239578318016984801869478851843
85861560789112949495459501737958331952853208805511
12540698747158523863050715693290963295227443043557
66896648950445244523161731856403098711121722383113
62229893423380308135336276614282806444486645238749
30358907296290491560440772390713810515859307960866
70172427121883998797908792274921901699720888093776
65727333001053367881220235421809751254540594752243
52584907711670556013604839586446706324415722155397
53697817977846174064955149290862569321978468622482
83972241375657056057490261407972968652414535100474
82166370484403199890008895243450658541227588666881
16427171479924442928230863465674813919123162824586
17866458359124566529476545682848912883142607690042
24219022671055626321111109370544217506941658960408
07198403850962455444362981230987879927244284909188
84580156166097919133875499200524063689912560717606
05886116467109405077541002256983155200055935729725
71636269561882670428252483600823257530420752963450

この1000桁の数字から13個の連続する数字を取り出して、それらの総乗を計算する。では、それら総乗のうち最大となる値はいくらか。

例：6桁の数123789から5個の連続する数字を取り出す場合、 $1 \times 2 \times 3 \times 7 \times 8$と$2 \times 3 \times 7 \times 8 \times 9$の二通りとなり、後者の$2 \times 3 \times 7 \times 8 \times 9=3024$が最大の総乗となる。

$20 \times 20$ の格子のうち, 斜めに並んだ4つの数字が赤くマークされている.

08 02 22 97 38 15 00 40 00 75 04 05 07 78 52 12 50 77 91 08
49 49 99 40 17 81 18 57 60 87 17 40 98 43 69 48 04 56 62 00
81 49 31 73 55 79 14 29 93 71 40 67 53 88 30 03 49 13 36 65
52 70 95 23 04 60 11 42 69 24 68 56 01 32 56 71 37 02 36 91
22 31 16 71 51 67 63 89 41 92 36 54 22 40 40 28 66 33 13 80
24 47 32 60 99 03 45 02 44 75 33 53 78 36 84 20 35 17 12 50
32 98 81 28 64 23 67 10 26 38 40 67 59 54 70 66 18 38 64 70
67 26 20 68 02 62 12 20 95 63 94 39 63 08 40 91 66 49 94 21
24 55 58 05 66 73 99 26 97 17 78 78 96 83 14 88 34 89 63 72
21 36 23 09 75 00 76 44 20 45 35 14 00 61 33 97 34 31 33 95
78 17 53 28 22 75 31 67 15 94 03 80 04 62 16 14 09 53 56 92
16 39 05 42 96 35 31 47 55 58 88 24 00 17 54 24 36 29 85 57
86 56 00 48 35 71 89 07 05 44 44 37 44 60 21 58 51 54 17 58
19 80 81 68 05 94 47 69 28 73 92 13 86 52 17 77 04 89 55 40
04 52 08 83 97 35 99 16 07 97 57 32 16 26 26 79 33 27 98 66
88 36 68 87 57 62 20 72 03 46 33 67 46 55 12 32 63 93 53 69
04 42 16 73 38 25 39 11 24 94 72 18 08 46 29 32 40 62 76 36
20 69 36 41 72 30 23 88 34 62 99 69 82 67 59 85 74 04 36 16
20 73 35 29 78 31 90 01 74 31 49 71 48 86 81 16 23 57 05 54
01 70 54 71 83 51 54 69 16 92 33 48 61 43 52 01 89 19 67 48

(7行めの26から右下に63,78,14を赤くしたい)

それらの数字の積は $26 \times 63 \times 78 \times 14 = 1788696$ となる.

上の $20 \times 20$ の格子のうち, 上下左右斜めのいずれかの方向で連続する4つの数字の積のうち最大のものはいくつか?

三角数の数列は自然数の和で表わされ, 7番目の三角数は $1 + 2 + 3 + 4 + 5 + 6 + 7 = 28$ である. 三角数の最初の10項は:

$1, 3, 6, 10, 15, 21, 28, 36, 45, 55, \dots$

となる.

最初の7項について, その約数を列挙すると, 以下のとおり.

1: 1 3: 1,3 6: 1,2,3,6 10: 1,2,5,10 15: 1,3,5,15 21: 1,3,7,21 28: 1,2,4,7,14,28

これから, 7番目の三角数である28は, 5個より多く約数をもつ最初の三角数であることが分かる.

では, 500個より多く約数をもつ最初の三角数はいくつか.

正の整数に以下の式で繰り返し生成する数列を定義する.

n → n/2 (n が偶数)

n → 3n + 1 (n が奇数)

13からはじめるとこの数列は以下のようになる.

$13 → 40 → 20 → 10 → 5 → 16 → 8 → 4 → 2 → 1$

13から1まで10個の項になる. この数列はどのような数字からはじめても最終的には 1 になると考えられているが, まだそのことは証明されていない(コラッツ問題)

さて, 100万未満の数字の中でどの数字からはじめれば最長の数列を生成するか.

注意: 数列の途中で100万以上になってもよい

素数を小さい方から6つ並べると 2, 3, 5, 7, 11, 13 であり、6番目の素数は 13 である。

10 001 番目の素数を求めよ。

$2^{15} = 32768$ であり, 各位の数字の和は $3 + 2 + 7 + 6 + 8 = 26$ となる.

同様にして, $2^{1000}$ の各位の数字の和を求めよ.

注: 問題20も各位の数字の和に関する問題です。解いていない方は解いてみてください。

1 から 5 までの数字を英単語で書けば one, two, three, four, five であり, 全部で $3 + 3 + 5 + 4 + 4 = 19$ の文字が使われている.

では 1 から 1000 (one thousand) までの数字をすべて英単語で書けば, 全部で何文字になるか.

注: 空白文字やハイフンを数えないこと. 例えば, 342 (three hundred and forty-two) は 23 文字, 115 (one hundred and fifteen) は20文字と数える. なお, "and" を使用するのは英国の慣習.

以下の50桁の数字100個の合計の上から10桁を求めなさい。

37107287533902102798797998220837590246510135740250
46376937677490009712648124896970078050417018260538
74324986199524741059474233309513058123726617309629
91942213363574161572522430563301811072406154908250
23067588207539346171171980310421047513778063246676
89261670696623633820136378418383684178734361726757
28112879812849979408065481931592621691275889832738
44274228917432520321923589422876796487670272189318
47451445736001306439091167216856844588711603153276
70386486105843025439939619828917593665686757934951
62176457141856560629502157223196586755079324193331
64906352462741904929101432445813822663347944758178
92575867718337217661963751590579239728245598838407
58203565325359399008402633568948830189458628227828
80181199384826282014278194139940567587151170094390
35398664372827112653829987240784473053190104293586
86515506006295864861532075273371959191420517255829
71693888707715466499115593487603532921714970056938
54370070576826684624621495650076471787294438377604
53282654108756828443191190634694037855217779295145
36123272525000296071075082563815656710885258350721
45876576172410976447339110607218265236877223636045
17423706905851860660448207621209813287860733969412
81142660418086830619328460811191061556940512689692
51934325451728388641918047049293215058642563049483
62467221648435076201727918039944693004732956340691
15732444386908125794514089057706229429197107928209
55037687525678773091862540744969844508330393682126
18336384825330154686196124348767681297534375946515
80386287592878490201521685554828717201219257766954
78182833757993103614740356856449095527097864797581
16726320100436897842553539920931837441497806860984
48403098129077791799088218795327364475675590848030
87086987551392711854517078544161852424320693150332
59959406895756536782107074926966537676326235447210
69793950679652694742597709739166693763042633987085
41052684708299085211399427365734116182760315001271
65378607361501080857009149939512557028198746004375
35829035317434717326932123578154982629742552737307
94953759765105305946966067683156574377167401875275
88902802571733229619176668713819931811048770190271
25267680276078003013678680992525463401061632866526
36270218540497705585629946580636237993140746255962
24074486908231174977792365466257246923322810917141
91430288197103288597806669760892938638285025333403
34413065578016127815921815005561868836468420090470
23053081172816430487623791969842487255036638784583
11487696932154902810424020138335124462181441773470
63783299490636259666498587618221225225512486764533
67720186971698544312419572409913959008952310058822
95548255300263520781532296796249481641953868218774
76085327132285723110424803456124867697064507995236
37774242535411291684276865538926205024910326572967
23701913275725675285653248258265463092207058596522
29798860272258331913126375147341994889534765745501
18495701454879288984856827726077713721403798879715
38298203783031473527721580348144513491373226651381
34829543829199918180278916522431027392251122869539
40957953066405232632538044100059654939159879593635
29746152185502371307642255121183693803580388584903
41698116222072977186158236678424689157993532961922
62467957194401269043877107275048102390895523597457
23189706772547915061505504953922979530901129967519
86188088225875314529584099251203829009407770775672
11306739708304724483816533873502340845647058077308
82959174767140363198008187129011875491310547126581
97623331044818386269515456334926366572897563400500
42846280183517070527831839425882145521227251250327
55121603546981200581762165212827652751691296897789
32238195734329339946437501907836945765883352399886
75506164965184775180738168837861091527357929701337
62177842752192623401942399639168044983993173312731
32924185707147349566916674687634660915035914677504
99518671430235219628894890102423325116913619626622
73267460800591547471830798392868535206946944540724
76841822524674417161514036427982273348055556214818
97142617910342598647204516893989422179826088076852
87783646182799346313767754307809363333018982642090
10848802521674670883215120185883543223812876952786
71329612474782464538636993009049310363619763878039
62184073572399794223406235393808339651327408011116
66627891981488087797941876876144230030984490851411
60661826293682836764744779239180335110989069790714
85786944089552990653640447425576083659976645795096
66024396409905389607120198219976047599490197230297
64913982680032973156037120041377903785566085089252
16730939319872750275468906903707539413042652315011
94809377245048795150954100921645863754710598436791
78639167021187492431995700641917969777599028300699
15368713711936614952811305876380278410754449733078
40789923115535562561142322423255033685442488917353
44889911501440648020369068063960672322193204149535
41503128880339536053299340368006977710650566631954
81234880673210146739058568557934581403627822703280
82616570773948327592232845941706525094512325230608
22918802058777319719839450180888072429661980811197
77158542502016545090413245809786882778948721859617
72107838435069186155435662884062257473692284509516
20849603980134001723930671666823555245252804609722
53503534226472524250874054075591789781264330331690

以下の三角形の頂点から下の行の隣接する数字を通って下まで移動するとき, その数値の和の最大値は23になる.

   3
  7 4
 2 4 6
8 5 9 3

(3,7,4,9という経路を赤くしめしたい）

この例では $3 + 7 + 4 + 9 = 23$.

以下の三角形を頂点から下まで移動するとき, その最大の和を求めよ.

              75
             95 64
            17 47 82
           18 35 87 10
          20 04 82 47 65
         19 01 23 75 03 34
        88 02 77 73 07 63 67
       99 65 04 28 06 16 70 92
      41 41 26 56 83 40 80 70 33
     41 48 72 33 47 32 37 16 94 29
    53 71 44 65 25 43 91 52 97 51 14
   70 11 33 28 77 73 17 78 39 68 17 57
  91 71 52 38 17 14 91 43 58 50 27 29 48
 63 66 04 68 89 53 67 30 73 16 69 87 40 31
04 62 98 27 23 09 70 98 73 93 38 53 60 04 23

注: ここではたかだか 16384 通りのルートしかないので, すべてのパターンを試すこともできる. Problem 67 は同じ問題だが100行あるので, 総当りでは解けない. もっと賢い方法が必要である.

(他ページへのリンク)

次の情報が与えられている.

• 1900年1月1日は月曜日である.

• 9月, 4月, 6月, 11月は30日まであり, 2月を除く他の月は31日まである.

• 2月は28日まであるが, うるう年のときは29日である.

• うるう年は西暦が4で割り切れる年に起こる. しかし, 西暦が400で割り切れず100で割り切れる年はうるう年でない.

20世紀（1901年1月1日から2000年12月31日）中に月の初めが日曜日になるのは何回あるか?

$n × (n - 1) × ... × 3 × 2 × 1$ を $n!$ と表す.

例えば, $10! = 10 × 9 × ... × 3 × 2 × 1 = 3628800$ となる. この数の各桁の合計は $3 + 6 + 2 + 8 + 8 + 0 + 0 = 27$ である.

では, $100!$ の各位の数字の和を求めよ.

注: 問題16も各位の数字の和に関する問題です。解いていない方は解いてみてください。

5000個以上の名前が書かれている46Kのテキストファイルnames.txtを用いる. まずアルファベット順にソートせよ.

のち, 各名前についてアルファベットに値を割り振り, リスト中の出現順の数と掛け合わせることで, 名前のスコアを計算する.

たとえば, リストがアルファベット順にソートされているとすると, COLINはリストの938番目にある. またCOLINは 3 + 15 + 12 + 9 + 14 = 53 という値を持つ. よってCOLINは 938 × 53 = 49714 というスコアを持つ.

ファイル中の全名前のスコアの合計を求めよ.

フィボナッチ数列は以下の漸化式で定義される:$F_n = F_{n-1} + F_{n-2}$, ただし $F_1 = 1, F_2 = 1$.

最初の12項は以下である.

• $F_1 = 1$

• $F_2 = 1$

• $F_3 = 2$

• $F_4 = 3$

• $F_5 = 5$

• $F_6 = 8$

• $F_7 = 13$

• $F_8 = 21$

• $F_9 = 34$

• $F_{10} = 55$

• $F_{11} = 89$

• $F_{12} = 144$

12番目の項, $F_{12}$が3桁になる最初の項である.

1000桁になる最初の項の番号を答えよ.

順列とはモノの順番付きの並びのことである. たとえば, 3124は数 1, 2, 3, 4 の一つの順列である. すべての順列を数の大小でまたは辞書式に並べたものを辞書順と呼ぶ. 0と1と2の順列を辞書順に並べると

012 021 102 120 201 210

になる.

0,1,2,3,4,5,6,7,8,9からなる順列を辞書式に並べたときの100万番目はいくつか?

単位分数とは分子が1の分数である. 分母が2から10の単位分数を10進数で表記すると次のようになる.

1/2 = 0.5 1/3 = 0.(3) 1/4 = 0.25 1/5 = 0.2 1/6 = 0.1(6) 1/7 = 0.(142857) 1/8 = 0.125 1/9 = 0.(1) 1/10 = 0.1

0.1(6)は 0.166666... という数字であり, 1桁の循環節を持つ. 1/7 の循環節は6桁ある.

d < 1000 なる 1/d の中で小数部の循環節が最も長くなるような d を求めよ.

リンク先は各 Award の受賞者一覧ページ, Project Euler サイトにログインした状態で閲覧可能です. 進行状況確認ページ(Progress)で表示されている表に準じています。統計ページ(Statistics)に表示される表とは並びが異なるのでご注意下さい。↑

Problem Solving Awards †

(* difficulty explorer, coquering difficultiesが増えている)

Forum Post Awards †

• この "Forum" とは正答後に閲覧, 投稿することができる問題, 解法, プログラミング議論用フォーラムのことです. Project Euler のサイトフォーラム, http://projecteuler.chat には問題についての質問フォーラムがありますが, これとは異なるので注意.

• 問題発表後, 冒頭100件の投稿が自動的に永久保存ポスト (permanent post) にされ, その後は最新100件の投稿より古い投稿は, 管理者が手動で永久保存ポストにしない限り, 自動的に削除されます.

• "kudo" とはいわゆる投稿評価ポイントです. 投稿者には問題毎に5個の kudo 投票権が与えられ, ためになる, 熟慮されていると思う投稿に投票することができます.

$2×2$ のマス目の左上からスタートした場合, 引き返しなしで右下にいくルートは 6 つある.

では, $20×20$ のマス目ではいくつのルートがあるか.

オイラーは以下の二次式を考案している:

この式は, をからまでの連続する整数としたときに40個の素数を生成する. しかし, のとき となり41で割り切れる. また, のときは であり明らかに41で割り切れる.

計算機を用いて, 二次式 という式が発見できた. これは から の連続する整数で80個の素数を生成する. 係数の積は, で である.

さて, として以下の二次式を考える (ここで は絶対値): 例えば である.

から始めて連続する整数で素数を生成したときに最長の長さとなる上の二次式の, 係数 の積を答えよ.

どの問題から始めるべきですか？

それはあなたのもつ背景知識によります。問題の一覧表が２つあります。には、最近公表された最新10問があります。あなたがProject Euler初心者なら、ここの問題の様々な問題の種類や難易度の感じをつかむために、から始めるのがよいでしょう。

初めの100問あたりは、おおむねそれ以降の問題より易しいと考えられます。アーカイブの問題の一覧表には、それぞれの問題を解いた人数を示しています。一般的に、問題を解いた人数が多いほど、その問題は易しいと言えるでしょう。さらに、難易度評価システムもどこから手を付けるかの目安になるでしょう。アーカイブの表は番号(ID)、解いた人数(Solved By)、難易度(Difficulty)順に並べ替えることができます。

プログラムを書いたのですが、計算が終わるのに何日もかかってしまいます。

そんなはずはありません。それぞれの問題は「1分ルール」に基づいて作られています。つまり、難しい問題の場合、正しいアルゴリズムを考えるのには何時間もかかるかもしれませんが、どんなに難しい問題であっても、効率的な実装ができれば、そこそこの性能のコンピュータでも1分以内に答えを算出できるようにしています。

計算時間が1分以上かかってしまうのはダメですか？

それは気にしなくてかまいませんが、問題に立ち戻ってアプローチを改善させる動機になります。問題を解くとその問題に関連する掲示板にアクセスできるようになるので、そこで他の人のやり方をみることができるということを覚えておいて下さい。

検索エンジンを使って問題を解いてもよいですか？

インターネットを使って検索することは奨励されています。それによって多くの問題の下に隠された数学的な宝物が見つかることがあるからです。しかし、アイデアを検索することと、他所のウェブサイトで見つけた答えをただ使うことは紙一重です。クロスワードの答えをコピー機で複写したならば、あなたは何も達成していません。

自分のプログラムを10回見直したのですが、それでも答えが間違っていると言われてしまいます。問題が間違っているのでは？

新しく発表された問題では小さな間違いが入り込むことが十分ありえます。あるいは言葉遣いが曖昧であったり、説明が十分でないのかもしれません。しかし, 多くの人が問題を解いている中でただ一人10回間違いに突き当たるのは、あなたが間違っているのにもかかわらず、何か他のことのせいにしている可能性が高いでしょう。

問題を解く上で何かヒントはありますか？

問題の細部を注意深く読み、与えられた例を心にとどめて下さい。問題の裏に潜むアイデアに触れるために紙とペンで実験をおこなってください。もしも問題のアイデアがあなたにとって初めてのものだったら、インターネットや本で背景知識を得て下さい。問題には何を参照すべきかのヒントが載っているはずです。簡単な場合のプログラムを書き、例に示されている結果と一致することを確認してください。問題を正確に理解し、正しい方向に向かっていることが確認できるでしょう。このような試行から、最終結果を計算するのにかかる時間を推定してください。もし, その時間が1分を大きく上回るようであるのならば、もう一度戦略を練り直して下さい。

レベルとアワードとは何ですか？

25問解答するごとにレベルが1つ上がっていき、これを短期間の目標にすることで励みとすることができます。アワードは様々な条件により獲得できます。獲得する方法を知りたければ、のページに行くと現在用意されているアワードの完全なリストを見ることができます。レベル、アワードともに、統計ページの画像をクリックすればレベル別、あるいは特定のアワードを獲得したメンバーを確認することができます。

それぞれの問題には掲示板があるとのことですが、なぜ私はアクセスできないのでしょう？

問題の掲示板は正答しないとアクセスできません。アクセスすれば、他のメンバーがどのように問題を解いたか、手法に対する議論を見ることができ、あなたの考えを共有することができます。

名声(Kudos)とは何ですか？

名声の目的は、役に立つ、有用で、よく練られた投稿を見つけたことを投稿者や他のメンバーに知らせることです。各問題の掲示板につき5まで名声ポイントを付与することができます。ですので本当に価値があると思う投稿にのみ使用してください。

議論スレッドにはなぜ消滅する投稿があるのですか?

最初の100件の投稿のみが自動的に永続化されます. その後は最新の100個の投稿のみが保持されます; 古い投稿は自動的に削除されます. ただし, もし素晴らしい投稿がされた場合は管理者がそれを永続化することがあるかもしれません. Kudosはメンバーが有益な投稿を見つけ, 保存すべきであると管理者に知らせることのできる便利な方法です.

他に議論できる場所はないですか?

ありますよ! 一般的な議論に参加したり, 問題の解法やプログラミングのアイデアを共有したり, ウェブサイトについての提案をしたり, 問題の大まかなヒントや解説について聞くために, メンバーが投稿できる設定になっている代わりのphpBBフォーラムがあります. フォーラムへのリンクは下記に, しかしProject Eulerのサイトのアカウントから自動的にフォーラムのアカウントが移行して作られるわけではないので, フォーラムでアカウントを作成する必要があることに注意してください.

このフォーラムでのあなたの投稿はすべてのメンバーに見えています, ですので問題の解き方を明確に暴露してしまうことが無いようよく考えて投稿する必要があることに注意してください.

問題XXXの解き方を十分会得しました, なので私の解き方をどこかに発表してもよいですか?

あなたはすでに自分の質問に答えているように思います. しばらくの間取り組んだ問題を解き明かした時のなるほど!という瞬間より素晴らしいものはありません. 他の人にもこの瞬間を楽しんでもらうために私たちの考えを共有したいという善意であることも多いでしょう. しかし残念ながら, それは読者のためにはなりません. 真の学習とは積極的なプロセスであり, また発見のひらめきを経験するまでの長い道のりが一体どのようなものであるかを垣間見ることでもあります. あなたの高じた自尊心によって他の方からその経験を奪ったりしないようお願いします.

どのようにProject Eulerと連絡を取ったらよいですか?

このプロジェクトが始まったきっかけは何ですか?

Project Eulerは誰が運営していますか?

新しい問題のアイデアはメンバーで出しあっています. そのアイデアは有能な数学者やプログラマーによって煮詰められます. 端的に言えば, これらの人々がProject Eulerの運営者です.

Project Eulerに寄付することはできますか?

もちろんできます! Project Eulerはメンバーの持ち出しで運営されています. もしあなたが問題を楽しんで, 何か恩返しがしたいと思ったら, 寄付して頂けるのは大歓迎です.

(公式のaboutページにPaypal寄付ボタンが置かれています)

免責事項

創設以来, 多くの人たちの協力により, ここ数年Project Eulerの人気が非常に高まっています.

参加者はたいてい自分の成績を自慢したがるものです. 問題ページに設置されている掲示板はその最適の場所になっています. しかしその一方で, 人気の高まりは, 別の目的を持った人たちを惹きつけています. 多くのサイトが上記掲示板の代わりにProject Eulerの問題に対する解答を発表しており, どういうわけかそれらの解答を収集し提出して成績を自慢している人がいるようです.

こうした人たちを, 独力でProject Eulerを解いている参加者と確実に区別することは不可能です. Project Eulerのランキングは, こういうものだと解釈すべきです: その問題にメンバーが解答を提出し, 解答チェックで確認された正答数を表示したもの. 自力で達成したんだ, ということはメンバー自分自身が一番よくわかっています. 競争することにあまり重点を置き過ぎてしまうと, Project Eulerの目的の1つである問題を解くという楽しみを台無しにしてしまいます. そしてまた, 実績に対するメンバーからのいかなるクレームに対しても, Project Eulerが信用性を立証することはできません. 仮に重要だとしても, そうしたクレームを立証するには第三者による別の手段が必要になるでしょう.

少数の参加者の意図にかかわらず, 愉しみや教育のために質の高い問題を提供し続けることがProject Eulerの最大の目的です.

ログイン時に問題一覧下部に表示される注意事項

注記: この問題が解けないんだけど、とProject Eulerに連絡してこないでください。「解けない」ということは、つまり「解けていない」ということです!

と について, を全て考えてみよう:

これらを小さい順に並べ, 同じ数を除いたとすると, 15個の項を得る:

で同じことをしたときいくつの異なる項が存在するか?

10未満の自然数のうち、3もしくは5の倍数であるものは3, 5, 6, 9の4つであり、これらの合計は23である。

同じようにして、1000未満の3か5の倍数である数の合計を求めよ。

$d(n)$ を $n$ の真の約数の和と定義する. (真の約数とは $n$ 以外の約数のことである. ) もし, $d(a) = b$ かつ $d(b) = a$ $(a ≠ b のとき)$ を満たすとき, $a$ と $b$ は友愛数(親和数)であるという.

例えば, 220 の約数は 1, 2, 4, 5, 10, 11, 20, 22, 44, 55, 110 なので $d(220) = 284$ である. また, 284 の約数は 1, 2, 4, 71, 142 なので $d(284) = 220$ である.

それでは10000未満の友愛数の和を求めよ.

驚くべきことに, 各桁を4乗した数の和が元の数と一致する数は3つしかない.

• $1634 = 1^4 + 6^4 + 3^4 + 4^4$

• $8208 = 8^4 + 2^4 + 0^4 + 8^4$

• $9474 = 9^4 + 4^4 + 7^4 + 4^4$

ただし, $1=1^4$は含まないものとする. これらの数の和は $1634 + 8208 + 9474 = 19316$ である.

各桁を5乗した数の和が元の数と一致するような数の総和を求めよ.

$49/98$は面白い分数である.「分子と分母からそれぞれ$9$を取り除くと, $49/98 = 4/8$ となり, 簡単な形にすることができる」と経験の浅い数学者が誤って思い込んでしまうかもしれないからである. (方法は正しくないが，$49/98$の場合にはたまたま正しい約分になってしまう．)

我々は $30/50 = 3/5$ のようなタイプは自明な例だとする.

このような分数のうち, 1より小さく分子・分母がともに2桁の数になるような自明でないものは, 4個ある.

その4個の分数の積が約分された形で与えられたとき, 分母の値を答えよ.

(言葉が微妙)

完全数とは, その数の真の約数の和がそれ自身と一致する数のことである. たとえば, 28の真の約数の和は, $1 + 2 + 4 + 7 + 14 = 28$ であるので, 28は完全数である.

真の約数の和がその数よりも少ないものを不足数といい, 真の約数の和がその数よりも大きいものを過剰数と呼ぶ.

12は, $1 + 2 + 3 + 4 + 6 = 16$ となるので, 最小の過剰数である. よって2つの過剰数の和で書ける最少の数は24である. 数学的な解析により, 28123より大きい任意の整数は2つの過剰数の和で書けることが知られている. 2つの過剰数の和で表せない最大の数がこの上限よりも小さいことは分かっているのだが, この上限を減らすことが出来ていない.

2つの過剰数の和で書き表せない正の整数の総和を求めよ.

すべての桁に $1$ から $n$ が一度だけ使われている$n$桁の数をパンデジタル (pandigital) であるということにしよう: 例えば5桁の数 15234 は1から5のパンデジタルである.

7254 は面白い性質を持っている. $39 × 186 = 7254$ と書け, 掛けられる数, 掛ける数, 積が1から9のパンデジタルとなる.

掛けられる数/掛ける数/積が1から9のパンデジタルとなるような積の総和を求めよ.

ヒント：いくつかの積は2通り以上の掛けられる数/掛ける数/積の組み合わせを持つが1回だけ数え上げよ.

イギリスでは硬貨はポンド$£$とペンス$p$があり，一般的に流通している硬貨は以下の8種類である.

$1p, 2p, 5p, 10p, 20p, 50p, £1 (100p), £2 (200p)$.

以下の方法で£2を作ることが可能である．

$1×£1 + 1×50p + 2×20p + 1×5p + 1×2p + 3×1p$

これらの硬貨を使って$£2$を作る方法は何通りあるか?

1から初めて右方向に進み時計回りに数字を増やしていき, 5×5の螺旋が以下のように生成される:

(表のかきかたと赤色文字)

両対角線上の数字の合計は101であることが確かめられる.

$1001×1001$の螺旋を同じ方法で生成したとき, 対角線上の数字の和はいくつか?

辺の長さが $\{a,b,c\}$ と整数の3つ組である直角三角形を考え, その周囲の長さを $p$ とする. $p = 120$のときには3つの解が存在する:

$\{20,48,52\}, \{24,45,51\}, \{30,40,50\}$

$p ≤ 1000$ のとき解の数が最大になる $p$ はいくつか?

197は巡回素数と呼ばれる. 桁を回転させたときに得られる数 197, 971, 719 が全て素数だからである.

100未満には巡回素数が13個ある: 2, 3, 5, 7, 11, 13, 17, 31, 37, 71, 73, 79, および97である.

100万未満の巡回素数はいくつあるか?

192 に 1, 2, 3 を掛けてみよう.

192 × 1 = 192 192 × 2 = 384 192 × 3 = 576

積を連結することで1から9のパンデジタル数 192384576 が得られる. 192384576 を 192 と (1,2,3) の連結積と呼ぶ.

(pediaへのリンク、ちょうど一回なら書くか？)

同じようにして, 9 を 1,2,3,4,5 と掛け連結することでパンデジタル数 918273645 が得られる. これは 9 と (1,2,3,4,5) との連結積である.

整数と との連結積として得られる9桁のパンデジタル数の中で最大のものはいくつか?

(2進) は10進でも2進でも回文数である.

100万未満で10進でも2進でも回文数になるような数の総和を求めよ.

(注: 先頭に0を含めて回文にすることは許されない.)

3797は面白い性質を持っている. まずそれ自身が素数であり, 左から右に桁を除いたときに全て素数になっている (3797, 797, 97, 7). 同様に右から左に桁を除いたときも全て素数である (3797, 379, 37, 3).

右から切り詰めても左から切り詰めても素数になるような素数は11個しかない. 総和を求めよ.

注: 2, 3, 5, 7を切り詰め可能な素数とは考えない.

正の整数を順に連結して得られる以下の10進の無理数を考える:

0.123456789101112131415161718192021...

(1文字おおきくして赤くする)

小数第12位は1である.

$d_n$で小数第$n$位の数を表す. $d_1 × d_{10} × d_{100} × d_{1000} × d_{10000} × d_{100000} × d_{1000000}$ を求めよ.

$145$は面白い数である. $1! + 4! + 5! = 1 + 24 + 120 = 145$となる.

各桁の数の階乗の和が自分自身と一致するような数の和を求めよ.

注: $1! = 1$ と $2! = 2$ は総和に含めてはならない.

n桁パンデジタルであるとは, 1からnまでの数を各桁にちょうど1つずつ持つこととする.

例えば2143は4桁パンデジタル数であり, かつ素数である. n桁（この問題の定義では9桁以下）パンデジタルな素数の中で最大の数を答えよ.

それぞれ2つの異なる素因数を持つ連続する2つの数が最初に現れるのは:

$14 = 2 × 7$ $15 = 3 × 5$

それぞれ3つの異なる素因数を持つ連続する3つの数が最初に現れるのは:

$644 = 2^2 × 7 × 23$ $645 = 3 × 5 × 43$ $646 = 2 × 17 × 19$

最初に現れるそれぞれ4つの異なる素因数を持つ連続する4つの数を求めよ. その最初の数はいくつか?

五角数は $P_n = n(3n-1)/2$ で生成される. 最初の10項は

$1, 5, 12, 22, 35, 51, 70, 92, 117, 145, \dots$

である.

$P_4 + P_7 = 22 + 70 = 92 = P_8$ である. しかし差 $70 - 22 = 48$ は五角数ではない.

五角数のペア $P_j$ と $P_k$ について, 差と和が五角数になるものを考える. 差を $D = |P_k - P_j|$ と書く. 差 $D$ の最小値を求めよ.

三角数の第$n$項は $t_n = n(n+1)/2$で与えられる. 最初の10項は

$1, 3, 6, 10, 15, 21, 28, 36, 45, 55, \dots$

である.

単語中のアルファベットを数値に変換した後に和をとる. この和を「単語の値」と呼ぶことにする. 例えば SKY は $19 + 11 + 25 = 55 = t_{10}$である. 単語の値が三角数であるとき, その単語を三角語と呼ぶ.

16Kのテキストファイル words.txt 中に約2000語の英単語が記されている. 三角語はいくつあるか?

数1406357289は0から9のパンデジタル数である（0から9が1度ずつ現れるので）。この数は部分文字列が面白い性質を持っている。

$d_1$を上位1桁目、$d_2$を上位2桁目の数とし、以下順に$d_n$を定義する。この記法を用いると次のことが分かる。

• $d_2d_3d_4=406$ は 2 で割り切れる

• $d_3d_4d_5=063$ は 3 で割り切れる

• $d_4d_5d_6=635$ は 5 で割り切れる

• $d_5d_6d_7=357$ は 7 で割り切れる

• $d_6d_7d_8=572$ は 11 で割り切れる

• $d_7d_8d_9=728$ は 13 で割り切れる

• $d_8d_9d_{10}=289$ は 17 で割り切れる

このような性質をもつ0から9のパンデジタル数の総和を求めよ。

三角数, 五角数, 六角数は以下のように生成される.

$T_{285} = P_{165} = H_{143} = 40755$であることが分かる.

次の三角数かつ五角数かつ六角数な数を求めよ.

素数41は6つの連続する素数の和として表せる:

$41 = 2 + 3 + 5 + 7 + 11 + 13$

100未満の素数を連続する素数の和で表したときにこれが最長になる.

同様に, 連続する素数の和で1000未満の素数を表したときに最長になるのは953で21項を持つ.

100万未満の素数を連続する素数の和で表したときに最長になるのはどの素数か?

125874を2倍すると251748となる. これは元の数125874と順番は違うがちょうど同じ数字からなる。

$2x, 3x, 4x, 5x, 6x$ が $x$ と同じ数字からなるような最小の正整数 $x$ を求めよ.

次の級数の和は, $1^1 + 2^2 + 3^3 + \dots + 10^{10} = 10405071317$ である.

では, $1^1 + 2^2 + 3^3 + \dots + 1000^{1000}$ の最後の10桁を求めよ.

公差3330の等差数列1487, 4817, 8147は次の2つの変わった性質を持つ.

• (i)3つの項はそれぞれ素数である.

• (ii)各項は他の項の置換で表される.

1, 2, 3桁の素数にはこのような性質を持った数列は存在しないが, 4桁の増加列にはもう1つ存在する.

それではこの数列の3つの項を連結した12桁の数を求めよ.

Christian Goldbachは全ての奇合成数は平方数の2倍と素数の和で表せると予想した.

$9 = 7 + 2×1^2$ $15 = 7 + 2×2^2$ $21 = 3 + 2×3^2$ $25 = 7 + 2×3^2$ $27 = 19 + 2×2^2$ $33 = 31 + 2×1^2$

後に, この予想は誤りであることが分かった.

平方数の2倍と素数の和で表せない最小の奇合成数はいくつか?

1の位が3である2桁の数9つを*3と記す。それらのうち、13, 23, 43, 53, 73, 83の6つは素数である。

56**3の第3桁と第4桁に同じ数字を当てはめる。この5桁の数は7つの素数をもつ最初の例である: 56003, 56113, 56333, 56443, 56663, 56773, 56993. よって, この族の最初の数である56003は, このような性質を持つ最小の素数である.

桁を同じ数で置き換えることで8つの素数が得られる最小の素数を求めよ. (注:連続した桁でなくても良い)

2の平方根は無限に続く連分数で表すことができる.

$\displaystyle \sqrt{2} = 1 + \frac{1}{2 + \frac{1}{2 + \frac{1}{2 + \dots}}} = 1.414213\dots$

最初の4回の繰り返しを展開すると以下が得られる.

$1 + \frac{1}{2} = \frac{3}{2} = 1.5$ $1 + \frac{1}{2 + \frac{1}{2}} = \frac{7}{5} = 1.4$ $1 + \frac{1}{2 + \frac{1}{2 + \frac{1}{2}}} = \frac{17}{12} = 1.41666\dots$ $1 + \frac{1}{2 + \frac{1}{2 + \frac{1}{2 + \frac{1}{2}}}} = \frac{41}{29} = 1.41379\dots$

次の3つの項は$99/70, 239/169, 577/408$である. 第8項は$1393/985$である. これは分子の桁数が分母の桁数を超える最初の例である.

最初の1000項を考えたとき, 分子の桁数が分母の桁数を超える項はいくつあるか?

47とその逆さ読みを足し合わせると$47 + 74 = 121$となり, 回文数になる.

全ての数が直ちに回文数になるわけではない. 349を考えよう,

1. $349 + 943 = 1292$,

2. $1292 + 2921 = 4213$

3. $4213 + 3124 = 7337$

349は, 3回の操作を経て回文数になる.

まだ証明はされていないが, 196のようないくつかの数は回文数にならないと考えられている. 逆さ読みを足すという操作を経ても回文数にならないものをLychrel数と呼ぶ. 先のような数の理論的な性質により, またこの問題の目的のために, Lychrel数でないと証明されていない数はLychrel数だと仮定する.

更に, 10000未満の数については，常に以下のどちらか一方が成り立つと仮定してよい.

1. 50回未満の操作で回文数になる

2. まだ誰も回文数まで到達していない

実際, 10677が50回以上の操作を必要とする最初の数である: 4668731596684224866951378664 (53回の操作で28桁のこの回文数になる).

驚くべきことに, 回文数かつLychrel数であるものが存在する. 最初の数は4994である.

10000未満のLychrel数の個数を答えよ.

Googol ($10^{100}$)は非常に大きな数である: 1の後に0が100個続く. $100^{100}$は想像を絶する. 1の後に0が200回続く. その大きさにも関わらず, 両者とも数字和 ( 桁の和 ) は1である.

$a, b < 100$ について自然数 $a^b$ を考える. 数字和の最大値を答えよ.

カードゲームのポーカーでは, 手札は5枚のカードからなりランク付けされている. 役を低い方から高い方へ順に並べると以下である.

• 役無し(ハイカード): 一番値が大きいカード

• ワン・ペア: 同じ値のカードが2枚

• ツー・ペア: 2つの異なる値のペア

• スリーカード: 同じ値のカードが3枚

• ストレート: 5枚の連続する値のカード

• フラッシュ: 全てのカードが同じスート (注: スートとはダイヤ・ハート・クラブ・スペードというカードの絵柄のこと)

• フルハウス: スリーカードとペア

• フォーカード: 同じ値のカードが4枚

• ストレートフラッシュ: ストレートかつフラッシュ

• ロイヤルフラッシュ: 同じスートの10, J, Q, K, A

ここでカードの値は小さい方から2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K, Aである. (訳注：データ中で10は'T'と表される)

もし2人のプレイヤーが同じ役の場合には, 役を構成する中で値が最も大きいカードによってランクが決まる: 例えば, 8のペアは5のペアより強い (下の例1を見よ). それでも同じランクの場合には (例えば, 両者ともQのペアの場合), 一番値が大きいカードによってランクが決まる (下の例4を見よ). 一番値が大きいカードが同じ場合には, 次に値が大きいカードが比べれられ, 以下同様にランクを決定する.

例:

poker.txtには1000個のランダムな手札の組が含まれている. 各行は10枚のカードからなる (スペースで区切られている): 最初の5枚がプレイヤー1の手札であり, 残りの5枚がプレイヤー2の手札である. 以下のことを仮定してよい

• 全ての手札は正しい (使われない文字が出現しない. 同じカードは繰り返されない)

• 各プレイヤーの手札は特に決まった順に並んでいるわけではない

• 各勝負で勝敗は必ず決まる

1000回中プレイヤー1が勝つのは何回か? (訳注 : この問題においてA 2 3 4 5というストレートは考えなくてもよい)

1から始めて, 以下のように反時計回りに数字を並べていくと, 辺の長さが7の渦巻きが形成される.

(表の書き方、素数を赤くする)

面白いことに, 奇平方数が右下の対角線上に出現する. もっと面白いことには, 対角線上の13個の数字のうち, 8個が素数である. ここで割合は8/13 ≈ 62%である.

渦巻きに新しい層を付け加えよう. すると辺の長さが9の渦巻きが出来る. 以下, この操作を繰り返していく. 対角線上の素数の割合が10%未満に落ちる最初の辺の長さを求めよ.

コンピュータの中では、文字にはそれぞれ一意のコードが割り当てられている。よく使われる標準としてASCII (American Standard Code for Information Interchange) がある。ASCIIでは、大文字のAは65、アスタリスク (*)は42, 小文字のkは107などと割り当てられている。

モダンな暗号化の方法として, テキストファイルの各バイトをASCIIに変換し, 秘密鍵から計算された値とXORを取るという手法がある. XOR関数の良い点は, 暗号化に用いたのと同じ暗号化鍵でXORを取ると平文を復号できる点である. 65 XOR 42 = 107であり, 107 XOR 42 = 65である.

破られない暗号化のためには, 鍵は平文と同じ長さのランダムなバイト列でなければならない. ユーザーは暗号文と暗号化鍵を別々の場所に保存する必要がある. また, もし一方が失われると, 暗号文を復号することは不可能になる.

悲しいかな, この手法はほとんどのユーザーにとって非現実的である. そこで, 鍵の変わりにパスワードを用いる手法が用いられる. パスワードが平文より短ければ (よくあることだが), パスワードは鍵として繰り返し用いられる. この手法では, 安全性を保つために十分長いパスワードを用いる必要があるが, 記憶するためにはある程度短くないといけない.

この問題での課題は簡単になっている. 暗号化鍵は3文字の小文字である. は暗号化されたASCIIのコードを含んでいる. また, 平文はよく用いられる英単語を含んでいる. この暗号文を復号し, 平文のASCIIコードの和を求めよ.

12345から3つ選ぶ選び方は10通りである.

123, 124, 125, 134, 135, 145, 234, 235, 245, 345.

組み合わせでは, 以下の記法を用いてこのことを表す: .

一般に, について である. ここで, と階乗を定義する.

になるまで, これらの値が100万を超えることはない: .

について, 100万を超える は何通りあるか?

5桁の数 $16807 = 7^5$は自然数を5乗した数である. 同様に9桁の数 $134217728 = 8^9$も自然数を9乗した数である.

自然数を $n$ 乗して得られる $n$ 桁の正整数は何個あるか?

素数3, 7, 109, 673は非凡な性質を持っている. 任意の2つの素数を任意の順で繋げると, また素数になっている. 例えば, 7と109を用いると, 7109と1097の両方が素数である. これら4つの素数の和は792である. これは, このような性質をもつ4つの素数の集合の和の中で最小である.

任意の2つの素数を繋げたときに別の素数が生成される, 5つの素数の集合の和の中で最小のものを求めよ.

三角数, 四角数, 五角数, 六角数, 七角数, 八角数は多角数であり, それぞれ以下の式で生成される.

3つの4桁の数の順番付きの集合 (8128, 2882, 8281) は以下の面白い性質を持つ.

1. この集合は巡回的である. 最後の数も含めて, 各数の後半2桁は次の数の前半2桁と一致する

2. それぞれ多角数である: 三角数 ($P_{3,127}=8128$), 四角数 ($P_{4,91}=8281$), 五角数 ($P_{5,44}=2882$) がそれぞれ別の数字で集合に含まれている

3. 4桁の数の組で上の2つの性質を持つのはこの組だけである.

三角数, 四角数, 五角数, 六角数, 七角数, 八角数が全て現れる6つの巡回する4桁の数からなる唯一の順序集合の和を求めよ.

平方根は連分数の形で表したときに周期的であり, 以下の形で書ける:

$\displaystyle \sqrt{N} = a_0 + \frac{1}{a_1 + \frac{1}{a_2 + \frac{1}{a3 + \dots}}}$

例えば, $\sqrt{23}$を考えよう.

$\displaystyle \sqrt{23} = 4 + \sqrt{23} - 4 = 4 + \frac{1}{\frac{1}{\sqrt{23} - 4}} = 4 + \frac{1}{1 + \frac{\sqrt{23} - 3}{7}}$

となる.

この操作を続けていくと,

$\displaystyle \sqrt{23} = 4 + \frac{1}{1 + \frac{1}{3 + \frac{1}{1 + \frac{1}{8 + \dots}}}}$

を得る.

操作を纏めると以下になる:

• $\displaystyle a_0 = 4, \frac{1}{\sqrt{23}-4} = \frac{\sqrt{23}+4}{7} = 1 + \frac{\sqrt{23}-3}{7}$

• $\displaystyle a_1 = 1, \frac{7}{\sqrt{23}-3} = \frac{7(\sqrt{23}+3)}{14} = 3 + \frac{\sqrt{23}-3}{2}$

• $\displaystyle a_2 = 3, \frac{2}{\sqrt{23}-3} = \frac{2(\sqrt{23}+3)}{14} = 1 + \frac{\sqrt{23}-4}{7}$

• $\displaystyle a_3 = 1, \frac{7}{\sqrt{23}-4} = \frac{7(\sqrt{23}+4}{7} = 8 + (\sqrt{23}-4)$

• $\displaystyle a_4 = 8, \frac{1}{\sqrt{23}-4} = \frac{\sqrt{23}+4}{7} = 1 + \frac{\sqrt{23}-3}{7}$

• $\displaystyle a_5 = 1, \frac{7}{\sqrt{23}-3} = \frac{7(\sqrt{23}+3)}{14} = 3 + \frac{\sqrt{23}-3}{2}$

• $\displaystyle a_6 = 3, \frac{2}{\sqrt{23}-3} = \frac{2(\sqrt{23}+3)}{14} = 1 + \frac{\sqrt{23}-4}{7}$

• $\displaystyle a_7 = 1, \frac{7}{\sqrt{23}-4} = \frac{7(\sqrt{23}+4)}{7} = 8 + (\sqrt{23}-4)$

よって, この操作は繰り返しになることが分かる. 表記を簡潔にするために, $\sqrt{23} = [4;(1,3,1,8)]$と表す. $(1,3,1,8)$のブロックは無限に繰り返される項を表している.

最初の10個の無理数である平方根を連分数で表すと以下になる.

• $\sqrt{2}=[1;(2)]$, 周期 1

• $\sqrt{3}=[1;(1,2)]$, 周期 2

• $\sqrt{5}=[2;(4)]$, 周期 1

• $\sqrt{6}=[2;(2,4)]$, 周期 2

• $\sqrt{7}=[2;(1,1,1,4)]$, 周期 4

• $\sqrt{8}=[2;(1,4)]$, 周期 2

• $\sqrt{10}=[3;(6)]$, 周期 1

• $\sqrt{11}=[3;(3,6)]$, 周期 2

• $\sqrt{12}= [3;(2,6)]$, 周期 2

• $\sqrt{13}=[3;(1,1,1,1,6)]$, 周期 5

$N ≤ 13$で奇数の周期をもつ平方根は丁度4つある.

$N ≤ 10000$ について奇数の周期をもつ平方根が何個あるか答えよ.

立方数 $41063625 \; (345^3)$は, 桁の順番を入れ替えると2つの立方数になる: $56623104 \; (384^3)$ と $66430125 \; (405^3)$ である. $41063625$は, 立方数になるような桁の置換をちょうど3つもつ最小の立方数である.

立方数になるような桁の置換をちょうど5つもつ最小の立方数を求めよ.

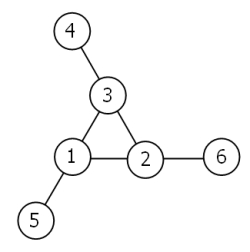
下に示す図のようなものを"magic" 3-gon ringという. これは1～6の数字を当てはめて, 各列の数字の和が9となっている. これを例として説明する.

外側のノードのうち一番小さいものの付いた列(例では4,3,2)から時計回りに回ってそれぞれ列の数字を3つ連ねて説明する. 例えば例のものは4,3,2; 6,2,1; 5,1,3という組で説明することができる.

1～6の数字を当てはめて, 各列の数字の和が等しくなるものは次の8通りある.

この組の各数字を連結して, 9桁の数字で表すことができる. 例えば, 上の図のものは4,3,2; 6,2,1; 5,1,3であるので432621513である.

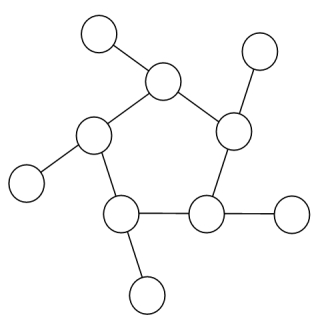
さて, 下の図に1～10の数字を当てはめ, 各列の数字の和が等しくなる"magic" 5-gon ringを作って, それを表す16桁または17桁の数字のうち, 16桁のものの最大の数字を答えよ.

(注, 3つの場合の例を見ても分かる通り, 列の始まりの数字を比べた時一番小さい数字で始まる列から時計回りに繋げるという条件のもとで文字列を生成する必要があります. この条件下で最大となる数字を答えてください. )

次の形式の, 2次のディオファントス方程式を考えよう:

$x^2 - Dy^2 = 1$

たとえば$D=13$のとき, $x$ を最小にする解は$649^2 - 13×180^2 = 1$である.

$D$が平方数のとき, 正整数のなかに解は存在しないと考えられる.

$D = \{2, 3, 5, 6, 7\}$に対して$x$を最小にする解は次のようになる:

• $3^2 - 2×2^2 = 1$

• $2^2 - 3×1^2 = 1$

• $9^2 - 5×4^2 = 1$(9を強調したい)

• $5^2 - 6×2^2 = 1$

• $8^2 - 7×3^2 = 1$

したがって,$D ≤ 7$に対して$x$を最小にする解を考えると,$D=5$のとき$x$は最大である.

$D ≤ 1000$に対する$x$を最小にする解で,$x$が最大になるような$D$の値を見つけよ.

2の平方根は無限連分数として書くことができる。

$\displaystyle \sqrt{2} = 1 + \frac{1}{2 + \frac{1}{2 + \frac{1}{2 + \frac{1}{2 + \dots}}}}$

この無限連分数を$\sqrt{2} = [1;(2)]$と表記することもできる。$(2)$は2が際限なく繰り返されることを示す。同様に$\sqrt{23} = [4;(1,3,1,8)]$である。

平方根の部分的な連分数の数列から良い有理近似が得られることが分かる.$\sqrt{2}$の近似分数について考えよう。

$\displaystyle 1 + \frac{1}{2} = \frac{3}{2}$

$\displaystyle 1 + \frac{1}{2 + \frac{1}{2}} = \frac{7}{5}$

$\displaystyle 1 + \frac{1}{2 + \frac{1}{2+\frac{1}{2}}} = \frac{17}{12}$

$\displaystyle 1 + \frac{1}{2 + \frac{1}{2+\frac{1}{2 + \frac{1}{2}}}} = \frac{41}{29}$

従って, $\sqrt{2}$の近似分数からなる数列の最初の10項は：

$\displaystyle 1, \frac{3}{2}, \frac{7}{5}, \frac{17}{12}, \frac{41}{29}, \frac{99}{70}, \frac{239}{169}, \frac{577}{408}, \frac{1393}{985}, \frac{3363}{2378}, \dots$

もっとも驚くべきことに, 数学的に重要な定数$e$は次のように表せて、 $e = [2; 1,2,1, 1,4,1, 1,6,1 , \dots , 1,2k,1, \dots]$

$e$ の近似分数からなる数列の最初の10項は：

$\displaystyle 2, 3, \frac{8}{3}, \frac{11}{4}, \frac{19}{7}, \frac{87}{32}, \frac{106}{39}, \frac{193}{71}, \frac{1264}{465}, \frac{1457}{536}, \dots$

第10項の近似分数の分子の桁を合計すると$1+4+5+7=17$である。

$e$についての連分数である近似分数の第100項の分子の桁の合計を求めよ。

下図の三角形の頂点から下まで移動するとき, その数値の合計の最大値は23になる。

   3
  7 4
 2 4 6
8 5 9 3

(3,7,4,9を強調したい)

この例では 3 + 7 + 4 + 9 = 23

100行からなる三角形を持つ15Kのテキストファイル triangle.txt （右クリックして、『名前をつけてリンク先を保存』）の上から下までの最大合計を見つけよ。

注：これは Problem 18のずっと難しいバージョンである。 全部で$2^{99}$通りの組み合わせがあるので、この問題を解くのに全ての経路を試すことは不可能である！ 毎秒1兆($10^{12}$)本の経路を調べることができたとしても、全てを調べるには200億年以上かかるだろう。 この問題を解く効率的なアルゴリズムがある ;o)

オイラーのトーティエント関数$φ(n)$(ファイ関数とも呼ばれる) とは,$n$未満の正の整数で$n$と互いに素なものの個数を表す. 例えば, 1, 2, 4, 5, 7, 8 は9未満で9と互いに素であるので,$φ(9) = 6$となる. 1 は全ての正の整数と互いに素であるとみなされる. よって$φ(1) = 1$である.

面白いことに,$φ(87109)=79180$であり, $87109$は$79180$を置換したものとなっている.

$1 < n < 10^7$で$φ(n)$が$n$を置換したものになっているもののうち,$n/φ(n)$が最小となる$n$を求めよ.

$n$と$d$を正の整数として, 分数$n/d$を考えよう.$n<d$かつ$\textrm{gcd}(n,d)=1$のとき, 真既約分数と呼ぶ.

(説明なくHCFだったが、ググるとgcdの別名らしいので。)

$d ≤ 8$について既約分数を大きさ順に並べると, 以下を得る:

1/8, 1/7, 1/6, 1/5, 1/4, 2/7, 1/3, 3/8, 2/5, 3/7, 1/2, 4/7, 3/5, 5/8, 2/3, 5/7, 3/4, 4/5, 5/6, 6/7, 7/8

3/7のすぐ左の分数は2/5である.

$d ≤ 1,000,000$について真既約分数を大きさ順に並べたとき, 3/7のすぐ左の分数の分子を求めよ.

オイラーのトーティエント関数$φ(n)$(ファイ関数とも呼ばれる) とは,$n$未満の正の整数で$n$と互いに素なものの個数を表す. 例えば, 1, 2, 4, 5, 7, 8 は9未満で9と互いに素であるので,$φ(9) = 6$となる.