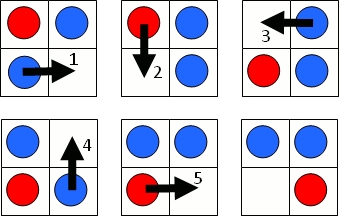
スライドパズルでは, カウンタを空白のスペースに向けて横または縦へスライドさせることができる. ゲームの目的は, 赤のカウンタを盤の左上角から右下角へ動かすことである；スペースはつねに右下角にある状態から始まる. 例えば次の一連の図は, $2×2$の盤にて5手でゲームを完了させる様子を示している.

$S(m,n)$を,$m×n$の盤でゲームを完了させる最小の手数を表すとする. 例えば,$S(5,4) = 25$であることが確かめられる.

$100$未満の素数$p$について,$S(m,n)=p^2$となる盤はちょうど 5482 個ある.

$10^6$未満の素数 p について,$S(m,n)=p^2$となる盤は何個あるか.

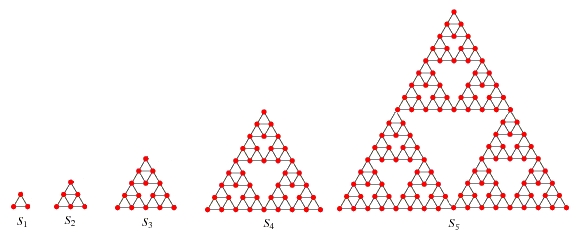
• 1次のシェルピンスキーグラフの三角形($S_1$)は正三角形である

• $S_{n+1}$は$S_n$3つをそれぞれのペアが角の頂点を一つ共有するように配置したものである

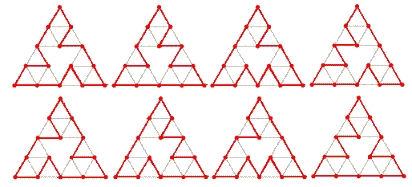
$C(n)$を$S_n$のすべての頂点を一度だけ通るような閉路の数とする. 例えば,$S_3$については下図のように8つの閉路が描けるため$C(3) = 8$となる.

であることが確認できる.

を求めよ.

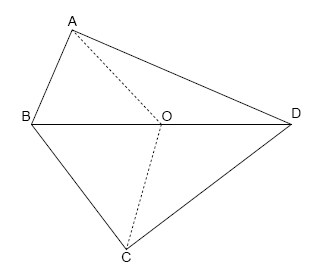
四角形$\textrm{ABCD}$は各辺の長さが整数で$1 \leq \textrm{AB} < \textrm{BC} < \textrm{CD} < \textrm{AD}$をみたす凸四角形である. $\textrm{BD}$の長さは整数である. $\textrm{O}$は$\textrm{BD}$の中点で,$\textrm{AO}$の長さも整数である. $\textrm{AO} = \textrm{CO} \leq \textrm{BO} = \textrm{DO}$となるこのような四角形$\textrm{ABCD}$をbiclinic整数四角形と呼ぶ.

例えば以下の四角形はbiclinic整数四角形である. $\textrm{AB} = 19, \textrm{BC} = 29, \textrm{CD} = 37, \textrm{AD} = 43, \textrm{BD} = 48, \textrm{AO} = \textrm{CO} = 23$となっている.

$B(N)$を $\textrm{AB}^2+\textrm{BC}^2+\textrm{CD}^2+\textrm{AD}^2 \leq N$ をみたす, 異なるbiclinic整数四角形$\textrm{ABCD}$の数とする. $B(10\,000) = 49, B(1\,000\,000) = 38239$であることが確かめられる.

$B(10\,000\,000\,000)$を求めよ.

爆竹が地上$100\,m$の高さで爆発する. 爆竹は爆発すると非常に細かい破片となり四方八方に初速$20 \, m/s$で広がる.

破片は空気抵抗を受けず,$g=9.81 \, m/s^2$で一定の重力場において動くものと仮定する.

破片が地面に到達するまでに動いた領域の体積($m^3$)を小数点以下4桁に丸めて答えよ.

Sam と Max は, ２個のデジタル時計を「デジタルルート（数字根）時計」に作り変えるよう依頼されている. デジタルルート時計は, 数字根をステップごとに計算するデジタル時計である.

時計に数字が与えられると, 時計は数字を表示し計算を開始する. 結果にたどりつくまでの途中の値がすべて表示される. 例えば, 時計に 137 という数が与えられると, "137"→"11"→"2" と表示してから真っ黒になり, 次の数を待つ.

各デジタル数字はセグメント状のライトから構成される：横セグメントが３本（上, 中, 下）と縦セグメントが４本（左上, 右上, 左下, 右下）である. 数 "1" は右上と右下の縦セグメントでできており, 数 "4" は中の横セグメントと, 左上, 右上, 右下の縦セグメントからできている. 数 "8" はすべてのセグメントが点灯する.

時計はセグメントを点灯/消灯させるときに限りエネルギーを消費する. "2" を点灯させるには 5 回の遷移を要する. "7" は 4 回だけ遷移を要する.

Sam と Max は２個の異なる時計を作る.

Sam の時計は 137 のような数を与えられると, "137" を表示し, パネルを消灯してから次の数（"11"）を点灯し, 再び消灯してそして最終的に最後の数（"2"）を点灯, しばらくして消灯する. たとえば, 137 では, Sam の時計は次のように動く.

• "137"：(2 + 5 + 4) × 2 = 22 回の遷移（"137" の点灯/消灯）

• "11" ：(2 + 2) × 2 = 8 回の遷移（"11" の点灯/消灯）

• "2"　　：(5) × 2 = 10 回の遷移（"2" の点灯/消灯）

合計で 40 回の遷移である.

Max の時計は異なる動きをする. パネル全体を消灯するのではなく, 次の数に必要のないセグメントのみを消灯するという賢いやり方である. 数 137 に対して, Max の時計は次のように動く.

• "137"：2 + 5 + 4 = 11 回の遷移（"137" の点灯） 　　　　　7 回の遷移（数 "11" に必要ないセグメントの消灯）

• "11" ：0 回の遷移（数 "11" はすでに正しく点灯済み） 　　　　　3 回の遷移（始めの "1" と２つ目の "1" の下部分を消灯； 　　　　　上部分は数 "2" と共通である）

• "2"　　：4 回の遷移（"2" にするため残りのセグメントを点灯） 　　　　　5 回の遷移（"2" を消灯）

合計で 30 回の遷移である.

もちろん, Max の時計のほうが Sam より電力の消費が少ない. ２つの時計にからの間の素数が与えられる. Sam の時計で必要な遷移の総数と Max の時計で必要な遷移の総数の差を求めよ.

実数$\sqrt{2}+\sqrt{3}$について考える. $\sqrt{2}+\sqrt{3}$の偶数乗を計算すると以下が得られる. $(\sqrt{2}+\sqrt{3})^2 = 9.898979485566356\dots$ $(\sqrt{2}+\sqrt{3})^4 = 97.98979485566356\dots$ $(\sqrt{2}+\sqrt{3})^6 = 969.998969071069263\dots$ $(\sqrt{2}+\sqrt{3})^8 = 9601.99989585502907\dots$ $(\sqrt{2}+\sqrt{3})^{10} = 95049.999989479221\dots$ $(\sqrt{2}+\sqrt{3})^{12} = 940897.9999989371855\dots$ $(\sqrt{2}+\sqrt{3})^{14} = 9313929.99999989263\dots$ $(\sqrt{2}+\sqrt{3})^{16} = 92198401.99999998915\dots$

これらの小数部分の先頭から連続している9の数は非減少であるように見える. 実際に$(\sqrt{2}+\sqrt{3})^{2n}$の小数部分は$n$を大きくすると$1$に近づいていくことが証明できる.

$p,q$を正の整数で$p<q$としたときに, $(\sqrt{p}+\sqrt{q})^{2n}$の小数部分が1に近づいていくような全ての実数$(\sqrt{p}+\sqrt{q})$について考える.

$C(p,q,n)$を$(\sqrt{p}+\sqrt{q})^{2n}$の小数部分の先頭から連続する9の数とする.

$N(p,q)$を$C(p,q,n) \geq 2011$となる最小の$n$とする.

についてを求めよ.

$x_1, x_2, \dots, x_n$を以下のような長さ$n$の数列とする.

• $x_1 = 2$

• $1 < i \leq n$について$x_{i-1} < x_i$

• $1 \leq i,j \leq n$について$(x_i)^j < (x_j+1)^i$

長さ2のこのような数列はの5つのみである. 長さ5のこのような数列は293ある. 以下がそのうちの3つの例である.

を長さのこのような数列の個数とする. である.

をで求めよ.

$N(i)$を$n!$が$(i!)^{1234567890}$で割り切れるような最小の整数$n$とする.

$S(u)$を$10 \leq i \leq u$に対し$S(u)=\sum N(i)$とする.

$S(1000)=614538266565663$である.

$S(1\, 000\, 000) \mod 10^{18}$を求めよ.

月が開拓され, 土地はただで手に入るようになったが, 困ったことがある. 確保した土地の周りに壁を作らなければならないのだが, 月に壁を作るにはお金がかかるのだ. 各国には$500\textrm{m} × 500 \textrm{m}$の正方形の土地が割り当てられているが, 壁の内側にある領域だけ保有することになる. 251001 本の杭が１メートル間隔で格子状に設置されている. 壁は閉じた一つながりの直線であり, 各直線は杭どうしを結んでいなければならない.

大きな国はもちろん$250,000\textrm{m}^2$の土地全体を囲うよう$2000\textrm{m}$の壁を建てた. グランドフェンウィック大公国は予算が厳しく, あなた（皇室プログラマ）に, 囲われた面積／壁の長さ の比が最大となる形はどのようなものか計算するよう依頼した.

あなたは紙の上で予備計算を行った.$2000\textrm{m}$の壁で$250,000\textrm{m}^2$の土地を囲うと, 囲われた面積／壁の長さの比は125となる. 認められてはいないが, いくらか良いかもしれないアイデアを試してみよう：正方形の内部に, 四辺に接するように円を置けば, 面積は $250^2\pi \textrm{m}^2$に等しく, 周囲の長さは$500\pi \textrm{m}$となり, したがって囲われた面積／壁の長さの比はこれも125となる.

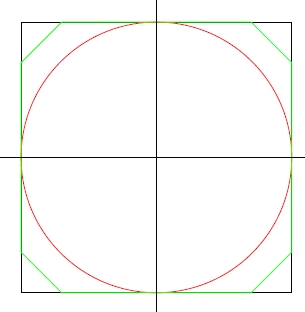
しかしながら, 三辺が75m, 75m, 75$\sqrt{2}$mの三角形を四つ正方形から切り離すと, 総面積は$238750\textrm{m}^2$で, 周囲の長さは$1400+300\sqrt{2}\textrm{m}$となる. したがって囲われた面積／壁の長さの比は130.87と著しく良くなる.

囲われた面積／壁の長さの比の最大値を求めよ. 答えを小数第９位で四捨五入し abc.defghijk の形で答えよ.

$p = p_1\, p_2\, p_3 \dots$を、$\{0,1,2,3,4,5,6,7,8,9\}$から等確率で選んだランダムな数字からなる無限の数字列とする。 $p$は実数$0.p_1 \, p_2 \, p_3 \dots$に対応することが分かる。 また、区間$[0,1)$からランダムに実数を選ぶことは、$\{0,1,2,3,4,5,6,7,8,9\}$から等確率で選んだランダムな数字からなる無限数字列を選ぶことと等価であることが分かる。

任意の$d$桁の正の整数$n$に対して、$p_k, p_{k+1}, \dots ,p_{k+d-1}$が$n$の十進表記と同じ順序で一致するような最小の添字を$k$とする。 また、$g(n)$を$k$の期待値とする。$g(n)$は常に有限であり、面白いことに、常に整数であることが示せる。

たとえば、$n = 535$なら、 $p = 31415926\underline{535}897\dots$に対して$k = 9$である。 $p = 35528714365004956000049084876408468\underline{535}4\dots$に対して$k = 36$である。 他も同様にして$g(535) = 1008$となることが分かる。

$\displaystyle \sum_{n=2}^{999} \, g \Big ( \Big \lfloor \frac{10^6}{n} \Big \rfloor \Big ) = 27280188$である。$\displaystyle \sum_{n=2}^{999999} \, g \Big ( \Big \lfloor \frac{10^{16}}{n} \Big \rfloor \Big )$を求めよ。

注： $\lfloor \cdot \rfloor$は床関数を表す。