331 : 十字返し

$N \times N$の円盤が正方形のゲーム盤に置かれている。円盤にはそれぞれ黒面と白面がある。

各手番では、円盤を１枚選び、同じ横列と同じ縦列にある円盤をすべて裏返す：ゆえに$2 \times N-1$枚の円盤が裏返される。すべての円盤が白面となればゲームは終了する。 次の例は$5 \times 5$の盤でのゲームを示している。

p331_crossflips3.gif

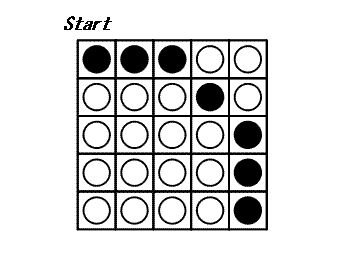
このゲームを終わらせる最小の手数は 3 であることが示せる.

$N \times N$の盤の左下の円盤を座標$(0,0)$とする。 右下の円盤は座標$(N-1,0)$で左上の円盤は座標$(0,N-1)$である。

$N \times N$枚の盤での次の配置を$C_N$とする： $N - 1 \leq \sqrt{x^2 + y^2}$を満たす$(x,y)$の円盤は黒面である；さもなくば白面である。$C_5$は上に示されている。

配置$C_N$から始めてゲームを終わらせる最小の手数を$T(N)$とする。配置$C_N$が解けない場合は$T(N)$は$0$である。 $T(5)=3$であることが分かる。また$T(10)=29, T(1000)=395253$である。

$\displaystyle \sum_{i=3}^{31} T(2^i-1)$を求めよ。