363 : ベジェ曲線 (*)

p363_bezier.png

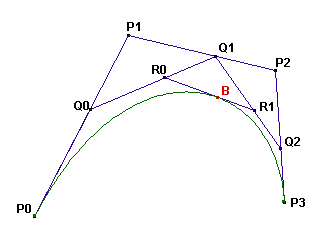
三次ベジェ曲線は四点$P_0, P_1, P_2, P_3$により定義される.

曲線は以下のように作られる : 線分$P_0P_1, P_1P_2, P_2P_3$上の点$Q_0, Q_1, Q_2$を, ($[0,1]$の範囲内の$t$に対し) $\displaystyle \frac{P_0Q_0}{P_0P_1}=\frac{P_1Q_1}{P_1P_2}=\frac{P_2Q_2}{P_2P_3}=t$となるように描く. 線分$Q_0Q_1, Q_1Q_2$上の点$R_0, R_1$を, 同じ値$t$を使って$\displaystyle \frac{Q_0R_0}{Q_0Q_1}=\frac{Q_1R_1}{Q_1Q_2}=t$となるように描く. 線分$R_0R_1$上の点$B$を同じ値$t$を使って$\displaystyle \frac{R_0B}{R_0R_1}=t$となるように描く. 点$P_0, P_1, P_2, P_3$によるベジェ曲線は, 線分$P_0P_1$上に取りうるすべての$Q_0$による, 点$B$の軌跡と定義される. ( 全ての点に対し$t$の値は同じであることに注意. )

(以下途中、アプレットをJSに作り替えよう)

右のアプレットで ( ※ 訳注 : こちらには Java アプレットを埋め込められないため, 公式にてご確認ください ) 点 P0, P1, P2, P3 をドラッグし, ベジェ曲線 (緑の曲線) がこれらの点によりどのように定義されるかを見ることができる. 線分 P0P1 の間にある点 Q0も同様にドラッグできる.

こうして作られたベジェ曲線は, $P_0$における線分$P_0P_1$と,$P_3$における線分$P_2P_3$とを接線に持つことがわかるだろう.

$P_0=(1,0), P_1=(1,v), P_2=(v,1), P_3=(0,1)$の三次ベジェ曲線は四分の一の円弧に近くなる. ここで0より大きい値$v$は線$OP_0, OP_3$と曲線によって囲まれる面積が π/4 ( 四分の一の円の面積 ) と等しくなるように選ばれる.

四分の一の円弧の長さに対しこの曲線の長さとの違いは何パーセントになるだろうか? つまり, $L$を曲線の長さとしたときの$\displaystyle 100 \times \frac{L-(\pi/2)}{(\pi/2)}$を計算せよ. 小数点以下11桁の位で四捨五入して答えよ.